
이전 포스팅에서 이항분포와 음이항분포를 R에서 간단하게 다루어보았습니다. 이번에는 이항분포와 음이항분포 문제들을 R로 풀어보면서 R에서 해당 함수들을 직접사용해보도록 하겠습니다.
1. 이항분포함수
- dbinom() : 이항분포의 확률값
| dbinom() 함수 파라미터 | |
| x | 성공횟수 |
| size | 시행횟수 |
| prob | B(n,p)에서 p값(단일 성공확률) |
- pbinom() : 이항분포의 누적확률값
| pbinom() 함수 파라미터 | |
| p | 누적확률을 얻을 분위수 |
| size | B(n,p)에서 n값 |
| prob | B(n,p)에서 p값(단일 성공확률) |
- qbinom() : 이항분포의 백분위수
| qbinom() 함수 파라미터 | |
| p | 분위수를 얻을 확률값 |
| size | B(n,p)에서 n값 |
| prob | B(n,p)에서 p값(단일 성공확률) |
- rbinom() : 이항분포를 따르는 난수발생
| rbinom() 함수 파라미터 | |
| n | 발생할 난수 개수 |
| size | B(n,p)에서 n값 |
| prob | B(n,p)에서 p값(단일 성공확률) |
문제1. 슛 성공률이 0.6인 어떤 농구선수가 10개의 슛을 날렸을 때, 성공한 슛의 개수를 X라한다. 다음을 구하여라
(1) 8번 슛을 성공할 확률은?
(2) 9개 이상 슛을 성공할 확률은?
(3) 이 선수는 평균적으로 몇개의 슛을 성공시키며 분산은 얼마인가?
<해답 R코드>
dbinom(x=8, size = 10, prob = 0.6) #문제 1번
sum(dbinom(x=9:10, size = 10, prob = 0.6))# 문제 2번
1 - pbinom(q=8, size = 10, prob = 0.6) #문제 2번
pbinom(q=8, size = 10, prob = 0.6, lower.tail = FALSE) #문제 2번
10*0.6 ; 10*0.6*0.4; #문제 3번

문제 1번은 이항분포를 해결해서 풀 수 있는 문제이며 (3)의 경우 3가지 방법을 이용해서 풀 수 있습니다.
lower.tail= FALSE를 설정하게되면 계산되는 확률이 P(X>K)입니다.
문제2. 어떤 국회의원이 한 구역에서 선거에 출마하려한다. 해당 구역의 선거권자 중 그를 지지하는 사람의 비율이 p=0.6이라 할 때, 8명의 선거권자를 임의로 뽑아 6명 이상이 그릴 지지할 확률은 얼마인가?
<해답 R코드>
# 문제2번 해답 (방법은 아래와 같이 3가지)
sum(dbinom(x=6:8, size= 8, prob = 0.6)) #방법1
1-pbinom(q=5, size = 8, prob = 0.6) #방법2
pbinom(q=5, size = 8, prob = 0.6, lower.tail = FALSE) #방법3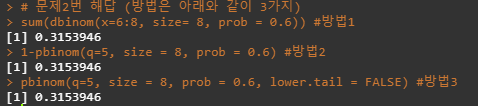
문제 1번과 같은 이항분포 문제풀이였습니다.
2. 음이항분포함수
- dnbinom() : 음이항분포의 확률값
| dnbinom() 함수 파라미터 | |
| x | 실패횟수(n-k) |
| size | 성공횟수 |
| prob | 단일시행 성공 확률 |
| mu | 음이항분포의 평균 |
- pnbinom() : 음이항 분포의 누적확률값
| pnbinom() 함수 파라미터 | |
| q | P(X<=x)에서 x값, x는 실패횟수 |
| size | 성공횟수 |
| prob | 단일시행 성공 확률 |
| lower.tail | FALSE일 때 P(X>x) |
- qnbinom() : 음이항분포의 분위수
| qnbinom() 함수 파라미터 | |
| p | 확률값 |
| size | 성공횟수 |
| prob | 단일시행 성공 확률 |
| lower.tail | FALSE일 때 P(X>x) |
- rnbinom() : 음이항분포를 따르는 난수생성
| rnbinom() 함수 파라미터 | |
| n | 생성할 난수의 갯수 |
| size | 성공횟수 |
| prob | 단일시행 성공확률 |
문제3. 어떤 인형뽑기기계에서 인형을 뽑을 수 있는 확률이 0.1이라 할 때, 3개의 인형을 뽑으려한다. 다음을 구하라
(1) 3개의 인형을 받기 위해 10번 게임을 할 확률은 얼마인가?
(2) 3개의 인형을 받기 위해 적어도 4번 게임을 할 확률은 얼마인가?
<해답 R코드>
dnbinom(x = 10-3, size= 3, prob = 0.1) #1번
1-dnbinom(x=3-3, size=3, prob = 0.1) #2번
pnbinom(q=3-3, size=3, prob = 0.1, lower.tail = FALSE) #2번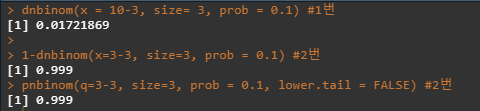
(2)번의 경우는 3개의 인형을 받기 위해 적어도 4번의 게임을 할 확률 즉 P(X>=4)를 구해주면 되는데
1-P(X<=3)을 구할 때 문제에서 요구하는 성공횟수가 3회 이므로 1-P(X=3)과 같습니다.
즉 한번도 실패하지않고 인형3개를 뽑을 확률만 1에서 빼주면된다. 따라서 pnbinom()의 q인자값 실패횟수는 0입니다.
'R + 통계' 카테고리의 다른 글
| [R 과 통계학 - 7] 이산확률분포(4) - 기하분포, 초기하분포, 포아송분포 (0) | 2020.07.15 |
|---|---|
| [R 과 통계학 - 5] 이산확률분포(2) - 베르누이분포, 이항분포, 음이항분포 (0) | 2020.07.14 |
| [R 과 통계학 - 4] 조건부 확률, 베이즈 정리 및 이산확률분포(1) (0) | 2020.07.14 |
| [R 과 통계학 - 3] R과 R Studio 설치 및 실행 (0) | 2020.07.14 |
| [R 과 통계학 - 2] 확률변수 및 순열과 조합 (0) | 2020.07.14 |

